アシタカの「生きろ、そなたは美しい」と「ブスは死ね」をめぐって-集合論的(数学的)に徹底分析を試みる-

「もののけ姫(スタジオジブリ公式)」は1997年に公開された宮崎駿監督による劇場用アニメーション作品である。
私は子供の頃に映画館に見に行くことができた幸運な世代だが、その後も見れば見るほど噛みしめるところのある作品だと思う。
今回はそんな「もののけ姫」の中でアシタカがサンに放った「生きろ、そなたは美しい」という現代的には多くの波紋を呼んでしまいそうな台詞について考えていこうと思う。
実際にこの台詞が生まれた状況を振り返ってみると、以下のような会話の中であった:
実のところ「生きろ、そなたは美しい」は、2つのパーツに別れたものがまとめて表現されているものであったという事になる。これだけでも少々問題はあるのだが、アシタカの台詞が波紋を呼ぶ根本原因は大きく2つ考えられる。
- 「生きろ、そなたは美しい」が「生きろ、なぜならそなたは美しいから」という意味なのか「生きろ、そしてそなたは美しい」なのかが判断しづらい、
- そして、「ブスは死ね」とか「ブスに生きる資格はない」というアシタカが直接言及していない対象についての辛辣な判断を感じ取ってしまうことがある。
今回は1997年のあの夏から続くこの大問題を集合論的(数学的)に分析し、最終的に「アシタカは概ねそんな酷いことを言っていないと考えるのが妥当である」ということを「証明」しようと思う。しちめんどくさい話にはなるが、順繰り話を進めていこう(なお、作品全体のあらすじや、カヤの小刀、神殺しの意味など、他の考察については「『もののけ姫』あらすじ・考察まとめ」で解説している)。
この記事の内容を、AIが対話形式(ラジオ形式)で分かりやすく解説してくれます。
問題設定、アプローチの方法、記号の準備と基本的な仮定
ここでは、基本的な問題設定やその問題へのアプローチの方法を明確にする。また、問題に取り組むために必要な記号と、妥当と思われる仮定を設定し問題を考察する準備を行う。
問題設定とアプローチの方法
基本的な問題設定は以下のようになる:
アシタカの言葉は「ブスは死ね」を意味するか?
この「問」に取り組む上で、まず最初に考えなければならないのは「生きろ、そなたは美しい」という言葉における「生きろ」と「美しい」の関係性である。アシタカの言葉には、
- 「生きろ、そしてそなたは美しい」
- 「生きろ、なぜならばそなたは美しいから」
という2つの捉え方がある。我々はアシタカにインタビューすることができないので、彼がどちらを意図したのかを確定させる事もできない(映画全体をみてもこれを確定することは不可能だと思う)。したがって、どちらの可能性も平等に扱わなければならない。
その上で、我々はアシタカの脳内宇宙、認識の世界について様々な可能性を考えなくてはならない。例えば、アシタカの認識する世界にそもそも「ブス」と呼ばれる人間が存在していなければ、問題の答えは「問題に意味がないという意味において『No』が答え」という事になるだろう。つまり、「アシタカはそんなこと言ってない」が答えになる。
したがって、アシタカが認識している世界における、「人」、「美しい人」、「ブス」、「生きるべき人」、「死ぬべき人」といった概念がどのような関係性にあるのかを網羅的に考察する必要があるので、そのようなアプローチで「問」に取り組むことにする。
それを集合論的、あるいは数学的に分析し切ろうと思うので、まずは記号の準備をしよう。
記号の準備と基本的な仮定
以下、次のような記号を用いる:
- $H:=$人全体の集合
- $L:=$生きるべき人全体の集合
- $D:=$死ぬべき人全体の集合
- $B:=$美しい人全体の集合
- $U:=$ブス全体の集合
- $I:= L^c \cap D^c$ (生きるべきでも死ぬべきでもない人全体の集合)
- $N:= B^c\cap U^c$ (美しくもないしブスでもない人全体の集合)
上の$H$、$L$、$D$、$B$、$U$、$I$、$N$はすべて「アシタカが認識する世界(アシタカの脳内宇宙)における」という修飾が省略されていることに注意する。
これらの集合の相互関係については、アシタカにインタビューしない限り厳密なことはわからないのだが、以下のような仮定を置くことは妥当なものだと思う:
- $L\cap D =\emptyset$ (生きるべきでありかつ死ぬべき人は存在しない)
- $B \cap U = \emptyset$ (美しくありかつブスという人は存在しない)
- $I \not =\emptyset$ (生きるべきでも死ぬべきでもない人が存在する)
- $N \not = \emptyset$ (美しくもなければブスでもない人が存在する)
人間の感情は複雑なので、ある程度の時間経過を前提にすると「あるときには生きるべきで、別のまたあるときには死ぬべき人」は存在するし、「美しいときもあればブスに見えることもある人」も存在しうるとは思う。
しかし、時間経過を十分短くとって眼の前の人に対する判断が一意的に決まる状況を考えれば、上の仮定①、②も妥当な仮定ということになるだろう(というより、①と②が妥当になる状況を考える)。
仮定③、④をまとめると「アシタカにとって『どうでもいい人』が存在している」ということになる。アシタカも人間だと思うので「認識はしているけど特段なんとも思っていない」人がいる仮定はむしろ妥当なものだと思う。
また、アシタカの台詞から以下のことが直ちに分かる:
アシタカの脳内宇宙において以下のことが成立する。
$B\not = \emptyset$ かつ $L\cap B \not=\emptyset$。
つまり、美しい人は存在し、美しくありかつ生きるべき人も存在している。
アシタカの台詞を「生きろ、そしてそなたは美しい」と解釈しても、「生きろ、なぜならばそなたは美しいから」と解釈しても、サンという存在が「美しい人」と「生きるべき人」の共通部分に存在していることになり、サンは「美しい人」なのだから $B$ の要素は少なくとも1つ存在するので、上の命題が成立する。
以下の文章では、仮定(Hyp)と上の命題が成立している状況を考えることにする。
アシタカが認識する世界における「美しい人」と「ブス」のあり方の可能性の考察
必要な準備が整ったので、ここからはアシタカの脳内宇宙の考察をしていくが、それでもなお場合分けが多く必要となる。大きくは、集合 $U$ が空集合かどうか(ブスが存在するかどうか)と $D$が空集合かどうか(「死ぬべき人」が存在するかどうか)で場合分けをすることにする。
Case 0. $\boldsymbol{U=\emptyset}$ (ブスは存在しない)
まずはアシタカの認識する世界にそもそも「ブス」は存在しない場合を考えるが、この場合はアシタカはブスについて何も言及しておらず、アシタカは単にサンに向かって
- 「生きろ、そしてそなたは美しい」
- 「生きろ、なぜならばそなたは美しいから」
のいずれかを言っただけということになる。もちろんどちらの意味で言ったかを確定することもできないが、特段彼の言葉の裏にある「ブス」についての思いを勘ぐる必要はない(「問」そのものに意味がない)。
結論としては大変素晴らしいが、$U=\emptyset$ (ブスは存在しない)という仮定は都合が良すぎるし現実離れしていると思われる。続いては$U\not = \emptyset$ (ブスは存在している)の場合を考える。
厳密な事を言うと、空集合はすべての集合の部分集合なので、$U = \emptyset$ のとき、$U \subset D$ は常に成立することになる。
つまり、論理学的には「ブスは死ね」($x \in U\Rightarrow x \in D$)という主張は真(正しい)ということになるのだが、この点に関してはAppendixで詳しく補足する。
Case 1. $\boldsymbol{U\not = \emptyset}$ かつ $\boldsymbol{D =\emptyset}$ (ブスは存在するが、死ぬべき人もいない)
続いて、アシタカの認識する世界に「ブスは存在するが、死ぬべき人もいない」という状況も考える。Case 0.と同じくらい理想的な状況ではあるが、この状況も可能性として考慮する必要はあるだろう。この場合はCase 1-1.からCase 1-5.までの場合を考察することになる。
Case 1-1. $\boldsymbol{B \subsetneq L}$ (生きるべき人に美しい人が真に含まれる)
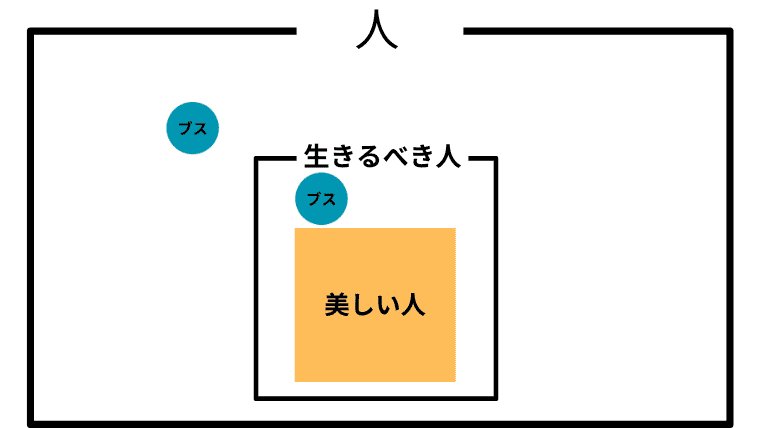
この場合の「美しい人」と「ブス」の取り扱い
この場合、アシタカにとって「美しい人であることは生きるべき人であるための十分条件」ということになり、「生きろそしてそなたは美しい」という表現と「生きろなぜならばそなたは美しい」という表現に差はないということになる(並列しても結果的に「美しい」が「生きる」の十分条件になる)。
また、アシタカにとって「ブス」は生きるべきかも知れないし、そうでもないかもしれない。そして、そもそもそれがアシタカの認識する人間のすべてなので、「ブスも人間」がアシタカにとっての「ブス」の取り扱いということになる。
Case 1-2. $\boldsymbol{L = B}$ (生きるべき人と美しい人が一致している)
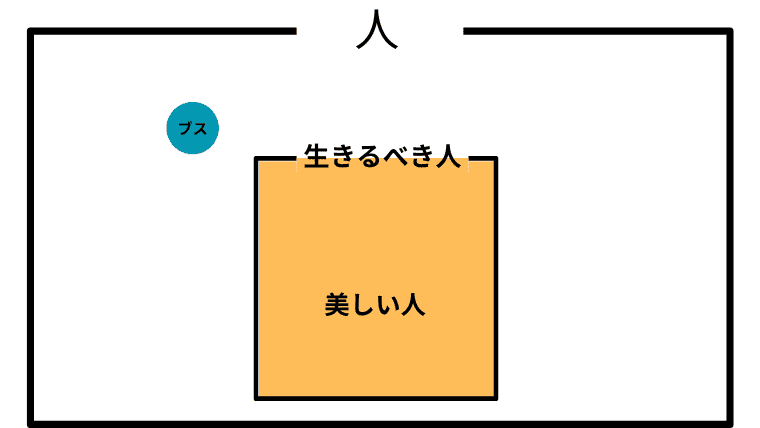
この場合の「美しい人」と「ブス」の取り扱い
この場合、アシタカにとって「美しいということと、生きるべきであることは同値」となる。相当強烈な状況ではあるが、この場合も、「生きろそしてそなたは美しい」という表現と「生きろなぜならばそなたは美しい」という表現に差はないということになる。
また、アシタカにとって「ブス」は生きるべきというほどではないが、死ぬべきということもない(死ぬべき人は存在しないので)。「ブスに生きてほしいと特段思わない」がアシタカにとっての「ブス」の取り扱いということになる。
さらに、「美しくもなければブスでもない普通の人」にも特段生きていてほしいとは思っていないということになる。しかし、死んでほしいとは思っていない。
Case 1-3. $\boldsymbol{L \cap B\not=\emptyset}$ かつ $\boldsymbol{L\setminus B \not= \emptyset}$ かつ $\boldsymbol{I \cap B \not=\emptyset}$ かつ $\boldsymbol{I \setminus B \not= \emptyset}$ (美しい人と生きるべき人に共通部分があり、生きるべき人が美しい人で尽くされず、美しい人の中にも生きるべきでない人が存在し、生きるべきでない人の中に美しくない人も存在する)
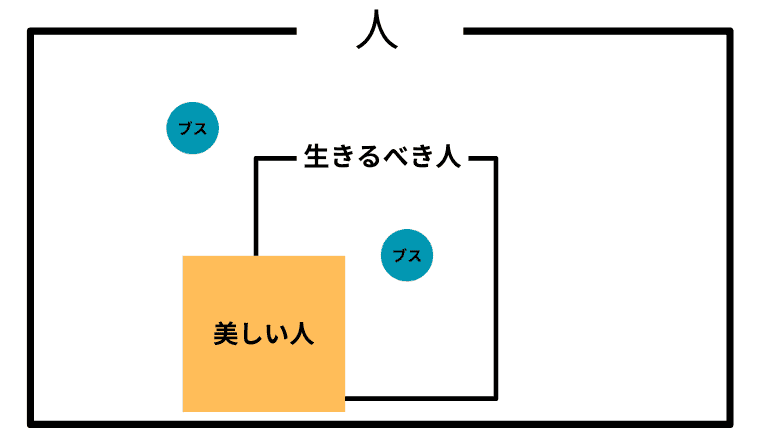
この場合の「美しい人」と「ブス」の取り扱い
この場合、アシタカは「美しい人の中にも生きるべき人とそうでない人がいる」と主張している。ある意味で最も「普通」な状況認識である。さらに、「美しい」ことが「生きるべき人」を必ずしも意味しないのだから「生きろ、なぜならばそなたは美しいから」という主張は成立しない。つまりアシタカは「生きろ、そしてそなたは美しい」と主張したことになる。
そして、アシタカにとって「ブス」は生きるべきかも知れないし、そうでもないかもしれない。つまり「ブスも人間」がアシタカにとっての「ブス」の取り扱いということになる。
Case 1-4. $\boldsymbol{L \subsetneq B}$ (生きるべき人を美しい人が真に含む)
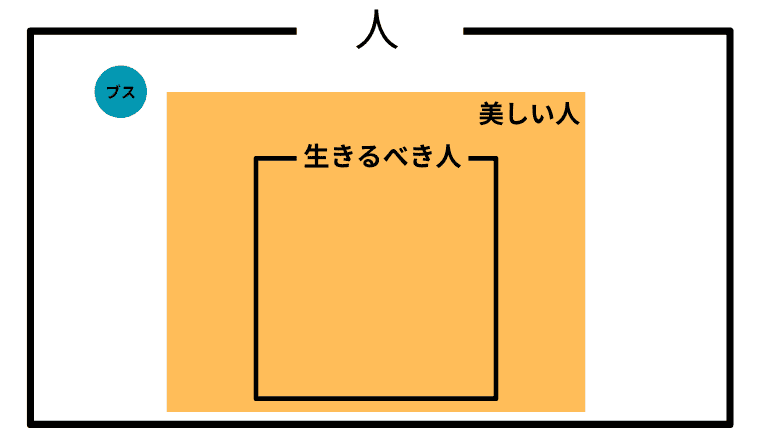
この場合の「美しい人」と「ブス」の取り扱い
この場合、アシタカは「生きるべき人はすべて美しい」と主張しており、アシタカにとって「美しい」の判断基準に「その人が生きるべきかどうか」が含まれることになる。この場合も「美しい」ことが「生きるべき」を必ずしも意味しないので、アシタカは「生きろ、そしてそなたは美しい」と主張したことになる。
また、アシタカにとって「ブス」は生きるべきというほどではないが、死ぬべきということもない。つまり「ブスに生きてほしいと特段思わない」がアシタカにとっての「ブス」の取り扱いということになる。
Case 1-5. $\boldsymbol{I \subsetneq B}$ かつ $\boldsymbol{L\cap B \not = \emptyset}$ (生きるべきとは言えない人を美しい人が含み、美しい人と生きるべき人に共通部分がある)
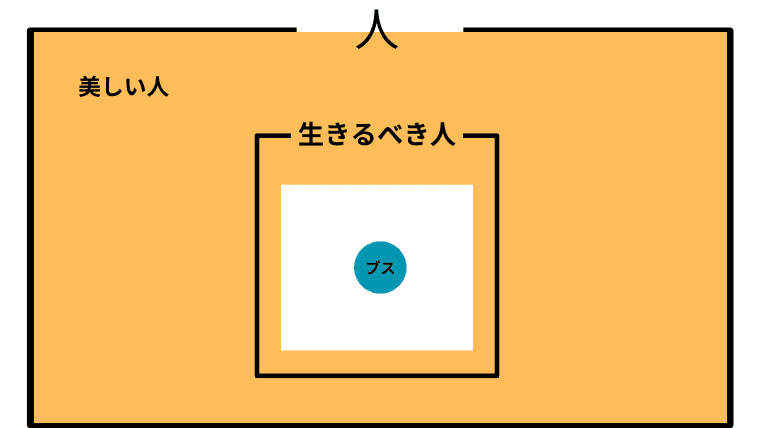
この場合の「美しい人」と「ブス」の取り扱い
この場合、アシタカは「美しい人は生きるべきかも知れないしそうでないかも知れない」と考えていることになり、アシタカは「生きろ、そしてそなたは美しい」と主張したことになる。
また、「ブス」は必然的に「生きるべき人」の一員ということになるので、「ブスこそ生きろ」がアシタカにとっての「ブス」の取り扱いということになる。
Case 2. $\boldsymbol{U\not = \emptyset}$ かつ $\boldsymbol{D\not=\emptyset}$ (ブスも死ぬべき人も存在している)
最後にアシタカの認識する世界に「ブスも存在しているし、死すべき人もいる」という最も問題が発生しそうな状況を考える。ここではCase 2-1.から Case 2-17.までの場合を考察することになる。
Case 2-1. $\boldsymbol{B \subsetneq L}$ (生きるべき人に美しい人が真に含まれる)
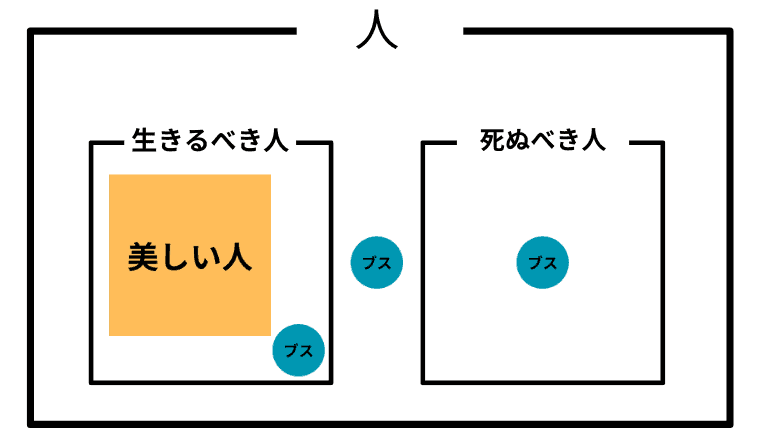
この場合の「美しい人」と「ブス」の取り扱い
この場合、アシタカにとって「美しいことは生きるべきであるための十分条件」ということになるので、「生きろ、そしてそなたは美しい」と「生きろ、なぜならそなたは美しいから」は同じ意味となる。
また、アシタカにとって「ブス」は生きるべきかも知れないし、死ぬべきかも知れないし、そのどちらでもないかも知れない。つまり「ブスも人間」がアシタカにとっての「ブス」の取り扱いということになる。
Case 2-2. $\boldsymbol{B = L}$ (生きるべき人と美しい人が一致)
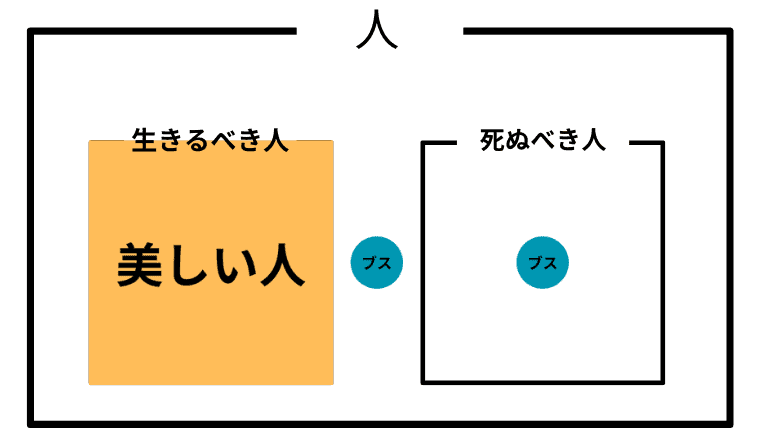
この場合の「美しい人」と「ブス」の取り扱い
この場合、アシタカにとって「生きるべき」と「美しい」は同じ意味になり、「生きろ、そしてそなたは美しい」と「生きろ、なぜならそなたは美しいから」も同じ意味となる。
また、アシタカにとって「ブス」は、死ぬべきかも知れないしそうでないかも知れないが、生きるべきと言うほどではないということになる。つまり「ブスは死んでも構わない」がアシタカにとっての「ブスの取り扱い」ということになる。
Case 2-3. $\boldsymbol{B \not \subset L}$ かつ $\boldsymbol{B\cap D = \emptyset}$ かつ $\boldsymbol{I\cap B \not=\emptyset}$ (美しい人が生きるべき人に含まれず、死ぬべき人とは共通部分がなく、美しいが生きるべきでも死ぬべきでない人が存在)
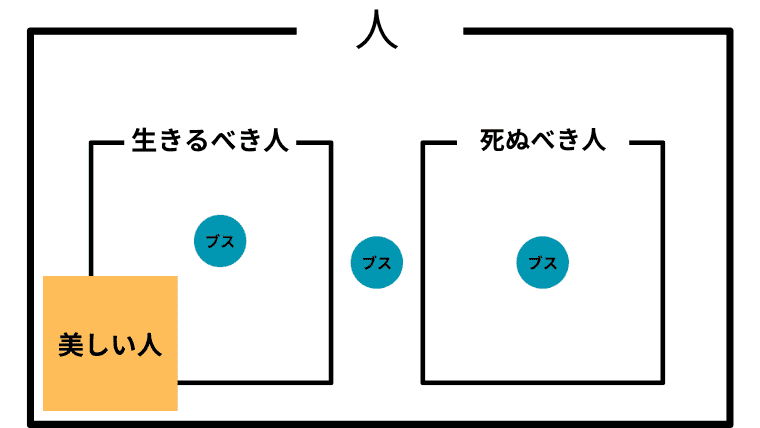
この場合の「美しい人」と「ブス」の取り扱い
この場合、アシタカは「美しいからといって生きるべきとは限らないが、美しい人が死ぬべきなんてことは決してない」と考えていることになる。美しい人がどれほど悪いことをしたとしても、美しいというだけで「死ぬべき」という強烈な判断を免れることになる(アシタカは根源的に「美しい人」に甘いということ)。
また「美しい」ということが必ずしも「生きるべき」を意味しないので、アシタカは「生きろ、そしてそなたは美しい」と主張したことになる。
そして、アシタカにとって「ブス」は生きるべきかも知れないし、死ぬべきかも知れないし、そのどちらでもないかも知れない。つまり「ブスも人間」がアシタカにとっての「ブス」の取り扱いということになる。
Case 2-4. $\boldsymbol{L \subsetneq B}$ かつ $\boldsymbol{B\cap D = \emptyset}$ かつ $\boldsymbol{D^c\not = B}$ (生きるべき人が美しい人に真に含まれ、死ぬべき人とは共通部分がなく、死ぬべき人の補集合とも一致しない)
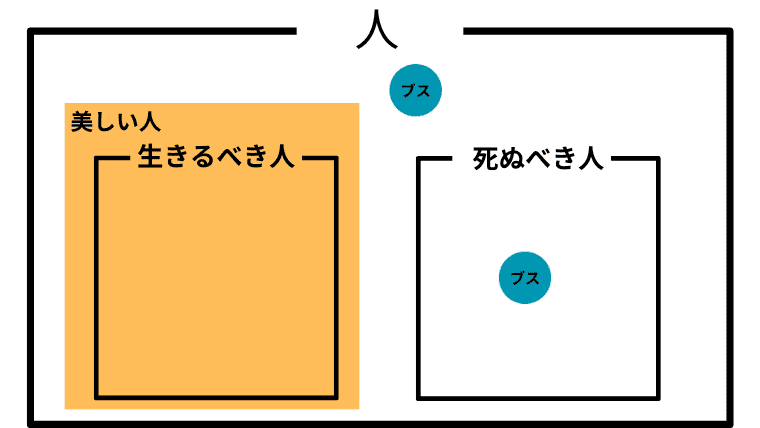
この場合の「美しい人」と「ブス」の取り扱い
この場合、アシタカにとって「生きるべきである」ことが「美しい」ことの判断基準の一つとなっていることになる。この場合も、「美しい」からと言って「生きるべき」とは必ずしもならないので、アシタカは「生きろ、そしてそなたは美しい」と主張したことになる。
また、アシタカにとって「ブス」は、死ぬべきかも知れないしそうでないかも知れないが、生きるべきと言うほどではないということになる。つまり「ブスは死んでも構わない」がアシタカにとっての「ブスの取り扱い」ということになる。
Case 2-5. $\boldsymbol{L\subset B}$ かつ $\boldsymbol{D \cap B \not =\emptyset}$ かつ $\boldsymbol{D\setminus B \not=\emptyset}$ かつ $\boldsymbol{I \not= B}$ かつ $\boldsymbol{I \cap B \not=\emptyset}$ (生きるべき人が美しい人に含まれ、死ぬべき人とも共通部分があり、どちらでもない人を美しい人が埋め尽くしていないが共通部分はある)
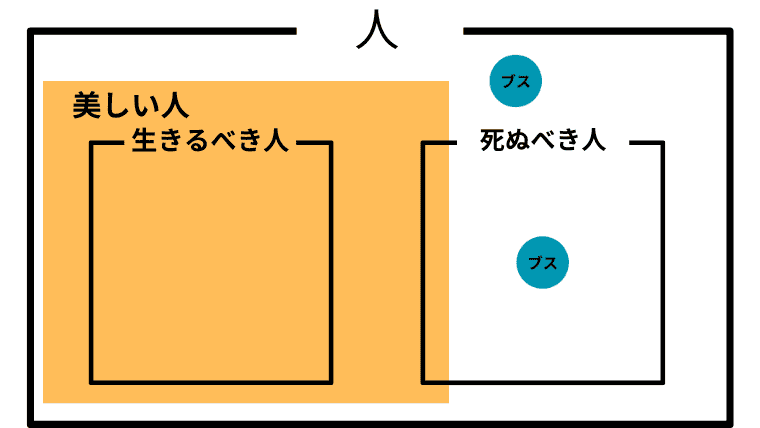
この場合の「美しい人」と「ブス」の取り扱い
この場合も、アシタカは「美しい人は、生きるべきかもしれないし、死ぬべきかもしれないし、そうでないかもしれない」と思っていることになる。つまり、「生きろ、そしてそなたは美しい」と主張したことになる。
また、アシタカにとって「ブス」は、死ぬべきかも知れないしそうでないかも知れないが、生きるべきと言うほどではないということになる。つまり「ブスは死んでも構わない」がアシタカにとっての「ブス」の取り扱いということになる。
Case 2-6. $\boldsymbol{D^c=B}$ (死ぬべきではない人が美しい人で尽くされており、美しい人には死ぬべき人がいない)
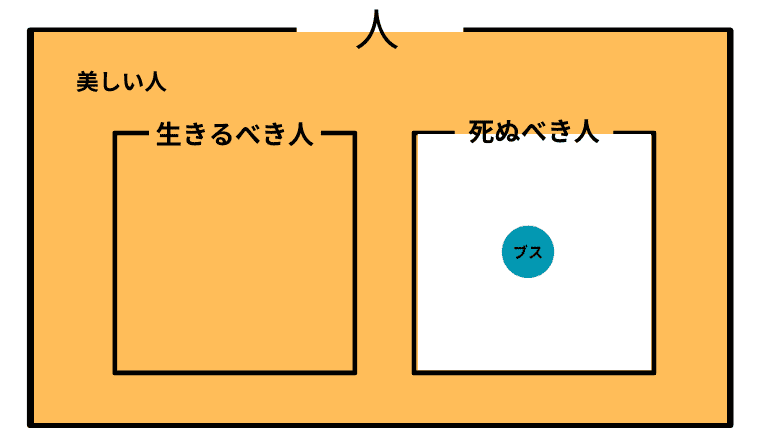
この場合の「美しい人」と「ブス」の取り扱い
この場合、アシタカは「美しい人は、生きるべきかもしれないし、そうでないかもしれないが、死ぬべきことはない」という認識をしており、「美しい」ということと「死ぬべきではない」ということが同じ意味をもつことになる。そして、「生きろ、そしてそなたは美しい」とアシタカは主張したことになる。
また、この場合、アシタカにとって「ブス」は、死ぬべき存在となってしまうので「ブスは死ね」がアシタカの「ブス」の取り扱いということになる。
Case 2-7. $\boldsymbol{D^c \subset B}$ かつ $\boldsymbol{B\cap D\not =\emptyset}$(美しい人が死ぬべき人の補集合を含み、美しい人にも死ぬべき人がいる)
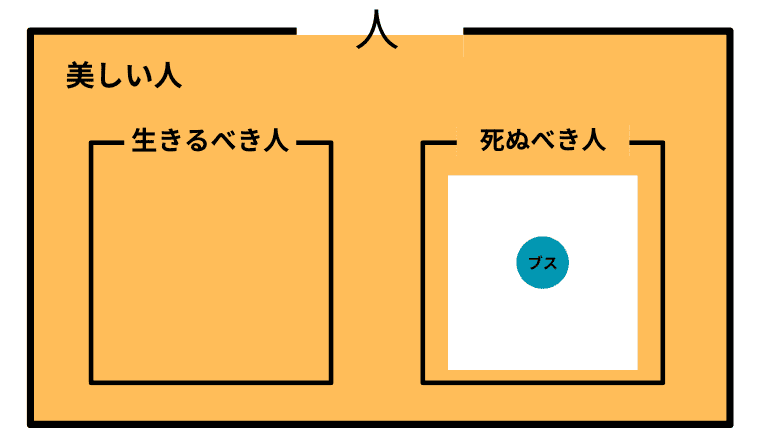
この場合の「美しい人」と「ブス」の取り扱い
この場合、アシタカは「美しい人は、生きるべきかもしれないし、死ぬべきかもしれないし、そうでないかもしれない」という至極真っ当なことを言っており、アシタカは「生きろ、そしてそなたは美しい」と主張したことになる。
そして、この場合もアシタカにとって「ブス」は、死ぬべき存在となってしまうので「ブスは死ね」がアシタカの「ブス」の取り扱いということになる。
Case 2-8. $\boldsymbol{D\subset B}$ かつ $\boldsymbol{L \cap B \not =\emptyset}$ かつ $\boldsymbol{L\setminus B \not=\emptyset}$ かつ $\boldsymbol{I \not= B}$ かつ $\boldsymbol{I \cap B \not=\emptyset}$ (死ぬべき人が美しい人に含まれ、生きるべき人とも共通部分があり、どちらでもない人を美しい人が埋め尽くしていないが共通部分はある)
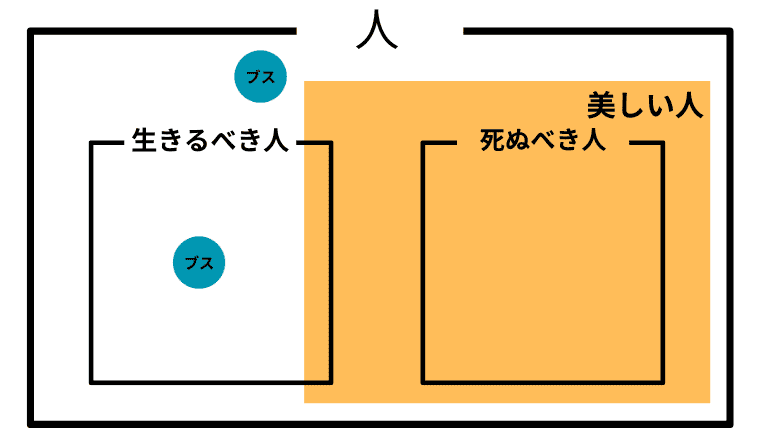
この場合の「美しい人」と「ブス」の取り扱い
この場合、アシタカは「美しい人は、生きるべきかもしれないし、死ぬべきかもしれないし、そうでないかもしれない」と考えていることになる。つまり、「生きろ、そしてそなたは美しい」と主張したことになる。
また、アシタカにとって「ブス」は、生きるべきかも知れないし、そうでもないかも知れないが死ぬべきというほどではないということになる。つまり「ブスこそ生きろ」がアシタカにとっての「ブス」の取り扱いということになる。
Case 2-9. $\boldsymbol{L^c \subset B}$ (生きるべき人以外を美しい人が埋め尽くし、生きるべき人の中に美しくない人もいる)
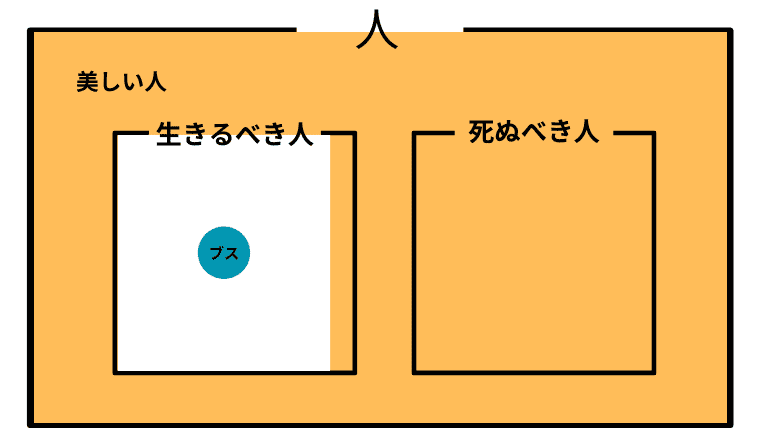
この場合の「美しい人」と「ブス」の取り扱い
この場合、アシタカは「美しい人は、生きるべきかもしれないし、死ぬべきかもしれないし、そうでないかもしれない」と考えていることになり、「生きろ、そしてそなたは美しい」と主張したことになる。
また、アシタカにとって「ブス」は生きるべき存在となっている。つまり「ブスも人間」がアシタカにとっての「ブスの取り扱い」ということになる。
Case 2-10. $\boldsymbol{L\setminus B \not =\emptyset}$ かつ $\boldsymbol{D\setminus B \not =\emptyset}$ かつ $\boldsymbol{D\cap B\not =\emptyset}$ かつ $\boldsymbol{I \cap B \not=\emptyset}$ かつ $I\not=B$ (美しい人と生きるべき人、死ぬべき人、どちらでもない人に共通部分があり、生きるべき人、死ぬべき人、どちらでもない人のいずれも美しい人で埋め尽くされていない)
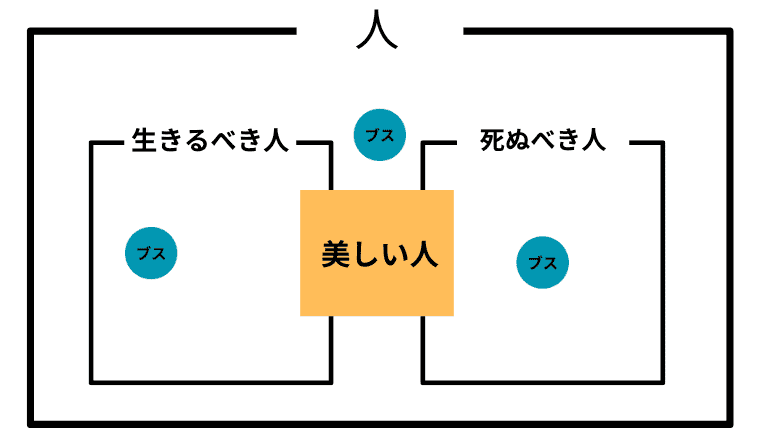
この場合の「美しい人」と「ブス」の取り扱い
この場合、アシタカは「美しい人は、生きるべきかもしれないし、死ぬべきかもしれないし、そうでないかもしれない」と考えていることになり、「生きろ、そしてそなたは美しい」と主張したことになる。
また、アシタカにとって「ブス」は生きるべきかも知れないし、死ぬべきかも知れないし、そのどちらでもないかも知れない。つまり「ブスも人間」がアシタカにとっての「ブスの取り扱い」ということになる。
Case 2-11. $\boldsymbol{L \cup D \subset B}$ かつ $\boldsymbol{I \not= B}$ かつ $\boldsymbol{I\cap B \not=\emptyset}$ (生きるべき人と死ぬべき人が美しい人に含まれ、どちらでもない人を美しい人が埋め尽くしていないが共通部分はある)
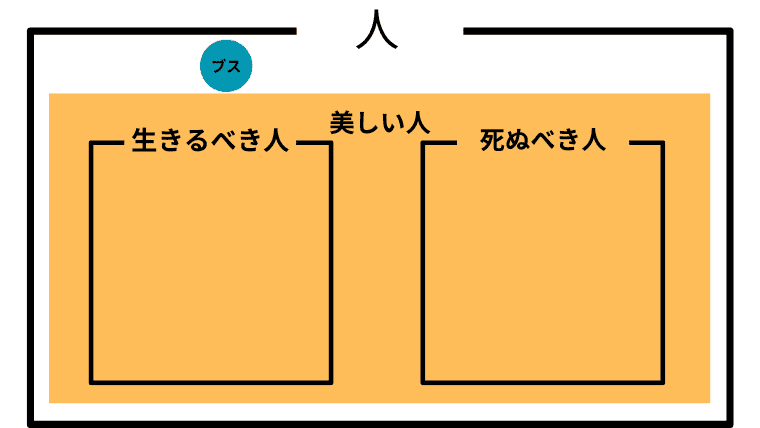
この場合の「美しい人」と「ブス」の取り扱い
この場合、「美しい人は、生きるべきかも知れないし、死ぬべきかも知れないし、そうでないかも知れないけど、生きるべきか死ぬべきかの判断対象になるのは美人だけ」ということになる。一応、アシタカは「生きろ、そしてそなたは美しい」と主張したことになる。
また、アシタカにとって「ブス」は、生きるべきということもないし、死ぬべきと言うほどでもない。つまり「ブスはどうでもいい」がアシタカにとっての「ブス」の取り扱いということになる。
Case 2-12. $\boldsymbol{B \subsetneq L\cup D}$ かつ $\boldsymbol{L\not = B}$ かつ $\boldsymbol{D \not = B}$ かつ $\boldsymbol{B\cap L \not=\emptyset}$ かつ $\boldsymbol{B \cap D\not = \emptyset}$ (美しい人が、生きるべき人と死ぬべき人にまるまる含まれており、生きるべき人と死ぬべき人のどちらも埋め尽くしていない)
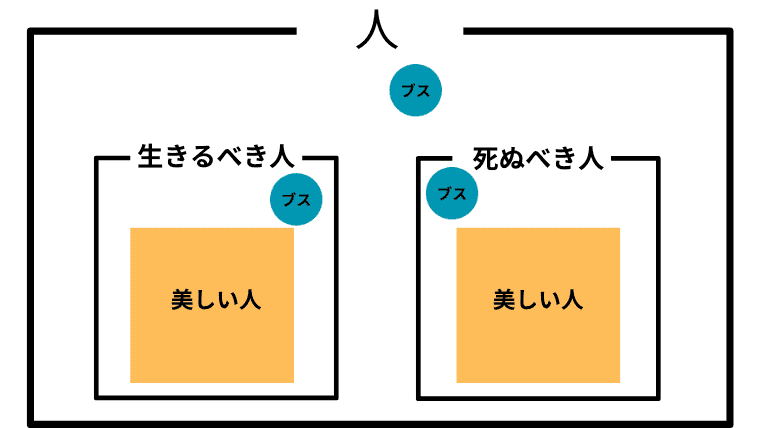
この場合の「美しい人」と「ブス」の取り扱い
この場合、「美しい人は、生きるか死ぬかのどちらか」ということになる。したがって、アシタカは「生きろ、そしてそなたは美しい」と主張したことになる。
また、アシタカにとって「ブス」は、生きるべきということもないし、死ぬべきと言うほどでもない。つまり「ブスも人間」がアシタカにとっての「ブス」の取り扱いということになる。
Case 2-13. $\boldsymbol{B \subsetneq L\cup D}$ かつ $\boldsymbol{L \setminus B =\emptyset}$ かつ $\boldsymbol{D \cap B \not= \emptyset}$ (美しい人が生きるべき人と死ぬべき人にまるまる含まれており、生きるべき人が埋め尽くされ、死ぬべき人を埋め尽くしていない)
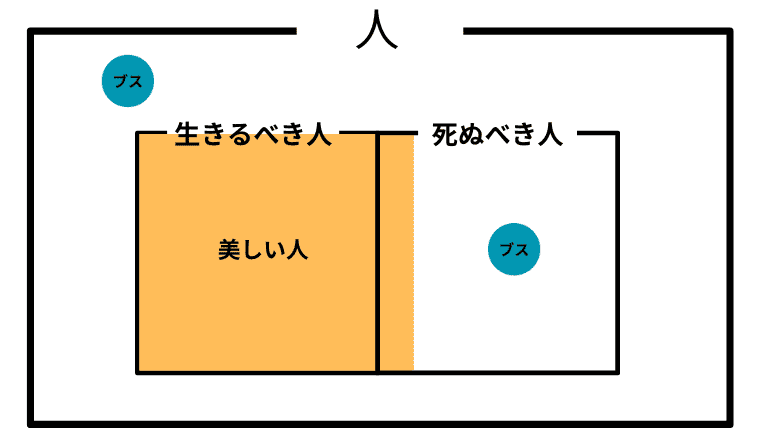
この場合の「美しい人」と「ブス」の取り扱い
この場合も、「美しい人は、生きるか死ぬかのどちらか」ということになり、アシタカは「生きろ、そしてそなたは美しい」と主張したことになる。
また、アシタカにとって「ブス」の中に生きるべき人はいないことになる。つまり「ブスは死んでも構わない」がアシタカにとっての「ブス」の取り扱いということになる。
Case 2-14. $\boldsymbol{B \subsetneq L\cup D}$ かつ $\boldsymbol{D \setminus B =\emptyset}$ かつ $\boldsymbol{L \cap B \not= \emptyset}$ (美しい人が生きるべき人と死ぬべき人にまるまる含まれており、死ぬべき人が埋め尽くされ、生きるべき人を埋め尽くしていない)
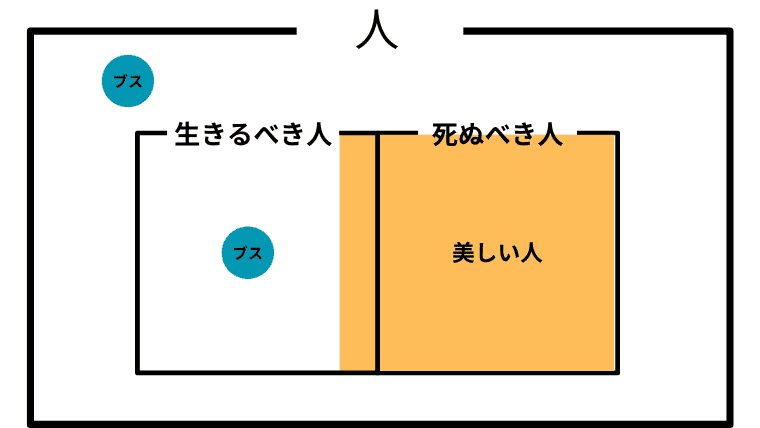
この場合の「美しい人」と「ブス」の取り扱い
この場合も、「美しい人は、生きるか死ぬかのどちらか」ということになり、アシタカは「生きろ、そしてそなたは美しい」と主張したことになる。
また、アシタカにとって「ブス」の中に死ぬべき人はいないことになる。つまり「ブスは死んではならない」がアシタカにとっての「ブス」の取り扱いということになる。
Case 2-15. $\boldsymbol{B = L\cup D}$ (生きるべき人と死ぬべき人全体が美しい人と一致している)
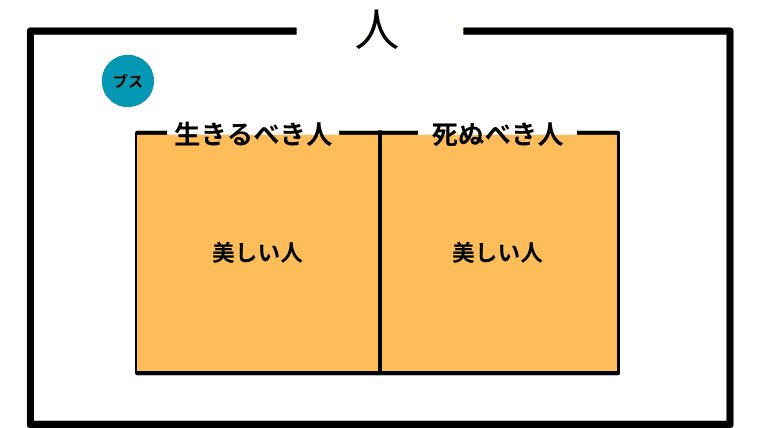
この場合の「美しい人」と「ブス」の取り扱い
この場合も、「美しい人は、生きるか死ぬかのどちらか」ということになり、アシタカは「生きろ、そしてそなたは美しい」と主張したことになる。
また、アシタカにとって「ブス」は生きるべきでもなければ死ぬべきでもない。つまり「ブスはどうでもいい」がアシタカにとっての「ブス」の取り扱いということになる。
Case 2-16. $\boldsymbol{I \subset B}$ かつ $\boldsymbol{L \cap B \not=\emptyset}$ かつ $\boldsymbol{L\setminus B \not =\emptyset}$ かつ $\boldsymbol{B\cap D \not = \emptyset}$ かつ $\boldsymbol{D\setminus B \not = \emptyset}$ (生きるべきでも死ぬべきでもない人を美しい人が埋め尽くしており、生きるべき人には美しい人もそうでないひともおり、死ぬべき人も同じ状況になっている)
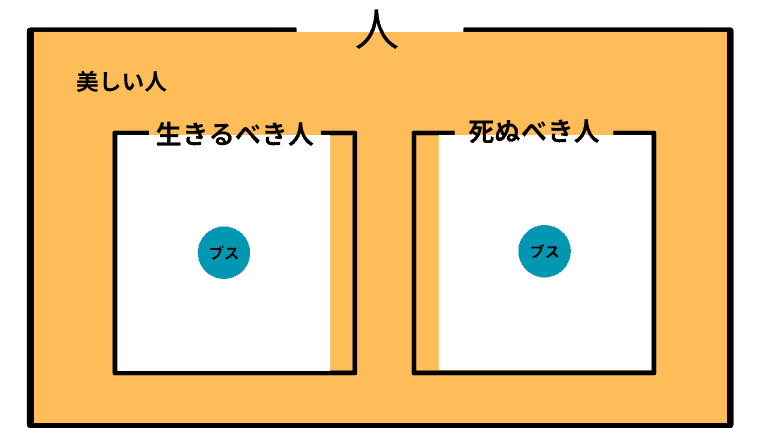
この場合の「美しい人」と「ブス」の取り扱い
この場合、アシタカは「美しい人は、生きるべきかも知れないし、死ぬべきかも知れないし、そうでないかも知れない」と認識していることになり、「生きろ、そしてそなたは美しい」と主張したことになる。
また、アシタカにとって「ブス」は生きるべきか死ぬべきかのどちらかということになる。つまり「ブスは無視できない」がアシタカにとっての「ブス」の取り扱いということになる。
Case 2-17. $\boldsymbol{I \subset B}$ かつ $\boldsymbol{L \cap B \not=\emptyset}$ かつ $\boldsymbol{L\setminus B \not=\emptyset}$ かつ $\boldsymbol{B\cap D \not = \emptyset}$ かつ $\boldsymbol{D\setminus B \not = \emptyset}$ (生きるべきでも死ぬべきでもない人を美しい人が埋め尽くしており、生きるべき人には美しい人もそうでないひともおり、死ぬべき人に美しい人はいない)
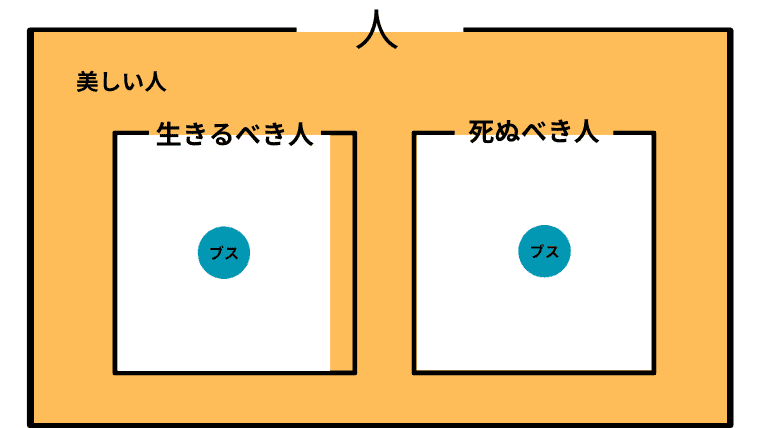
この場合の「美しい人」と「ブス」の取り扱い
この場合、アシタカは「美しい人は、生きるべきかも知れないし、そうでないかも知れないが、死ぬべき人はいない」と認識していることになり、「生きろ、そしてそなたは美しい」と主張したことになる。
また、アシタカにとって「ブス」は生きるべきか死ぬべきかのどちらかということになる。つまり「ブスは無視できない」がアシタカにとっての「ブス」の取り扱いということになる。
結論:アシタカは概ね「ブスは死ね」などと言っていない
それではここまで考えてきたことをまとめてみよう。アシタカの「生きろ、そなたは美しい」の意味と「ブス」の取り扱いの可能性の組み合わせは以下のようになる:
| 「生きろ、そなたは美しい」の解釈 | 「ブス」の取り扱い | 該当ケース番号 |
|---|---|---|
| どちらの意味で言ったか確定できない | 問題そのものに意味がない ※Appendix参照 |
Case 0 |
| 「生きろ、そしてそなたは美しい」と「生きろ、なぜならばそなたは美しいから」に差はない/同じ意味 | ブスも人間 | Case 1-1, Case 2-1 |
| 「生きろ、そしてそなたは美しい」と「生きろ、なぜならばそなたは美しいから」に差はない/同じ意味 | ブスに生きてほしいと特段思わない | Case 1-2 |
| 「生きろ、そしてそなたは美しい」と「生きろ、なぜならばそなたは美しいから」に差はない/同じ意味 | ブスは死んでも構わない | Case 2-2 |
| 「生きろ、そしてそなたは美しい」と主張 | ブスも人間 | Case 1-3, Case 2-3, Case 2-9, Case 2-10, Case 2-12 |
| 「生きろ、そしてそなたは美しい」と主張 | ブスに生きてほしいと特段思わない | Case 1-4 |
| 「生きろ、そしてそなたは美しい」と主張 | ブスこそ生きろ | Case 1-5, Case 2-8 |
| 「生きろ、そしてそなたは美しい」と主張 | ブスは死んでも構わない | Case 2-4, Case 2-5, Case 2-13 |
| 「生きろ、そしてそなたは美しい」と主張 | ブスは死ね | Case 2-6, Case 2-7 |
| 「生きろ、そしてそなたは美しい」と主張 | ブスはどうでもいい | Case 2-11, Case 2-15 |
| 「生きろ、そしてそなたは美しい」と主張 | ブスは死んではならない | Case 2-14 |
| 「生きろ、そしてそなたは美しい」と主張 | ブスは無視できない | Case 2-16, Case 2-17 |
上の表にあるように、アシタカが「ブスは死ね」と主張している可能性は確かに存在している。しかし、それは全23個(1+5+17=23)もあった可能性のうちたった2パターンの場合のみである。しかもその場合、アシタカは「生きろ、そしてそなたは美しい」と言っているだけで「生きろ、なぜならそなたは美しいから」といっているわけではない。
アシタカの脳内世界がCase 2-6. や Case 2-7.だったとしても「生きろ、そしてそなたは美しい」と明確に言ってくれていれば実のところ妙な勘ぐりは発生しなかったのではないだろうか(実際は「ブスは死ね」と認識しているけれど)。
さらにCase 2-6. や case 2-7.の場合、「美しくもなければブスでもない人」も死ぬべき人となり、「美しくなければ死ね」もアシタカの主張ということになってしまう。
しかし、この世界は通常「美しくはない人」によって埋め尽くされており「美しくなければ死ね」が実践された社会は瞬時に立ち行かなくなる。もちろん内面の真実のことであるので、アシタカがそんなことを考えている可能性はゼロではない。その一方で、アシタカがそのような極端な思想を持っている根拠になる描写もない。
そして、アシタカがそんな極端な思想を持っている状況は「常識的」には排除すべきものであり、そのような思想を持っていると主張するなら極めて慎重で深い調査が必要である(少なくともアシタカにインタビューをすべきである)。
以上の事をまとめると、以下のようになる:
アシタカが「ブスは死ね」と暗に主張していると言い張るにはもっと情報が必要であり、映画の描写だけではそのように結論づけることはできない。また、アシタカが「ブスは死ね」と考えている可能性は2/23という極めて低いものである上に「美しくなければ死ね」という極端な思想をアシタカが持っていることを前提にしなければならないので、常識的には排除していい可能性である。
一言でいうと、アシタカは概ね「ブスは死ね」などと言っていない。
一般アシタカ問題と予想の定式化
この記事では以下の「問」を考えた。
アシタカの言葉は「ブスは死ね」を意味するか?
ことの発端は「生きろ、そなたは美しい」という言葉が、何やら人の心にあらぬ勘ぐりを生み出してしまうことにある。しかし、この手の勘ぐりはアシタカの発言に限ったことではなく、日常生活の中で意外と頻発しているのではないだろうか。
そして、「勘ぐる」からにはよろしくないことを勘ぐっているわけで、ある人の発言からその人が直接は発言していないネガティブな意図を汲み取ってしまうことがある(あるいは、悪意を持って意識的に汲み取る)。
ただ、殆どの場合そのネガティブな意図を確定させることができるほどの情報が得られないと思うが、何かしらの情報があるにしても本当にそんな意図があるのかは慎重に判断する必要がある。つまり、我々は以下の問を常に心に止める必要があるだろう。
その人は、そんな酷いことを言っているのか?
そして、きちんとした詳細な調査を行えば、実のところアシタカ問題に対するこの記事の結論を超える結論が導けることを期待して、以下の予想を提出しよう。
その人は、そんな酷い事は言っていない。
ただ、上の主張だと少々強すぎで、予想が成立しているかどうかを確認するためには多くの調査と発言者のインタビューが必要となり、検証は大変(困難)だと考えられる。そこで、もう少し弱めた予想も提出する。
その人は概ねそんな酷い事は言っていないと考えるのが妥当である。
この予想なら、発言者本人に対するインタビュー等の調査をすることなく、この記事程度のことを考えれば主張の成立を示すことができると思われる。
他者の発言の裏を勘ぐって不愉快な気持ちになることは多々あると思うが、実のところ勝手な情報を付与して、勝手に不愉快になっているだけなのかもしれない。「アシタカ問題」についても「ブスは死ね」とアシタカが主張していると断定するには非常に強い仮定が必要になることが明らかになったと思う。
他者の発言以外でも、「早起きは三文の得」という言葉は「遅く起きたら負債を背負う」を意味しないし、TVドラマの刑事がイケメンだからといって我々が巨悪と戦ってはいけないわけではない、そして、「美少女戦士セーラームーン」という作品の存在は「美しくなければ世界を救ってはならない」ということを意味しない。
おそらく我々が住むこの世界は、あとほんの少しだけ美しいものであり、あの人もきっと悪意を持って言葉を使っているわけではない。
私自身は「予想1」が成立していると、強く期待している。希望的観測ではあるが。
Appendix: $\boldsymbol{U = \emptyset}$ の場合の補足
Case 0.の「メモ」に書いたように、$U = \emptyset$ の場合「ブスは死ね」という主張は真(正しい)ということになるのだが、実は $U\subset L$ も成立するため「ブスこそ生きろ」も正しい主張になる。したがって、「アシタカがブスについてどう考えているかを勘ぐるだけ無駄」であり、「問」が実質的な意味を持っていないことになる。
これはいわゆる「歴史にタラレバはない」という話に近い状態となっている。例えば次の主張は「正しい」だろうか「間違っている」だろうか:
「日本軍がミッドウェー海戦に勝利していたら、今頃世界は日本のものになっていた。」
単純に論理学的な視点に立つとこの主張は「正しい」ということになる。上の主張の前提条件である「日本軍がミッドウェー海戦に勝利」という主張が「偽(正しくない)」ので、その後にどんな主張をしても論理学的には「正しい」という判断になる。以下のようなものもすべて「真(正しい)」と判断される:
- 「日本軍がミッドウェー海戦に勝利していたら、私は自分の背中の翼で空を飛べるようになっていた。」
- 「日本軍がミッドウェー海戦に勝利していたら、巨人が日本列島を太平洋のど真ん中に移動させていた。」
- 「日本軍がミッドウェー海戦に勝利していたら、今頃恐竜が復活して世界を再び支配していた。」
- 「日本軍がミッドウェー海戦に勝利していたら、ドラえもんと友だちになっていた。」
つまり、論理学的には「真(正しい)」のだが、その主張を取り上げるだけ無駄ということになる。「歴史にタラレバはない」という言葉は様々な意味合いを持っていると思うが、上のような「どんなことでも主張しうるし、それに反論はできないので、タラレバを考えることで無駄な時間を過ごすな」という側面もある。
もちろん「タラレバ」を考えることは面白いことなので、私もそういうことを考えたりするが、それは「面白いだけ」であって、人と議論すべきことではないということを心得るべきである。
$U=\emptyset$ の場合にも論理学的には「ブスは死ね」は正しいことになってしまうが、「問」がそもそもナンセンス(意味がない)になっているのだから何も考える必要はないのである。
この記事では「生きろ、そなたは美しい」という台詞の真意について考察したが、本作の詳細なあらすじや、もう一つの大きな謎である「アシタカがカヤの小刀をサンにあげた理由」など、作品全体の解説については「『もののけ姫』あらすじ・考察まとめ」で網羅している。
この記事で使用した画像は「スタジオジブリ作品静止画」の画像です。
この記事を書いた人
最新記事





































